Prozentrechnung
Bei der Prozentrechnung geht es um Anteile vom Ganzen. „Anteile vom Ganzen“ das habt ihr bestimmt schon mal gehört, genau, bei der Bruchrechnung. Auch dort geht es um Anteile vom ganzen. Oder anders ausgedrück, die Prozentrechnung ist ein Teil der Bruchrechnung.
Geschichtliches
In früheren Zeiten wurden Anteile in Brüchen angegeben. Ein bekanntes Beispiel ist der Zehnt. Dies war im Mittelalter eine Abgabe an die Kirche oder auch an den Grundbesitzer. Ein Zehntel der geernteten Früchte und aufgezogenen Tiere waren als eine Art Steuer abzugeben. Auf Schiffen bekamen die Seeleute oft auch einen bestimmten Anteil des Fangs oder des Gewinns nach dem Verkauf des Handelsgutes. Der Kapitän bekam den größten Anteil, die anderen Seeleute je nach Job einen kleineren Anteil. Auf Walfängern z.B. 1/300 für einen Matrosen und 1/10 für den Kapitän.
Den Zehnt kann man noch sehr einfach durch abzählen bestimmen. Aber im laufe des Mittelalters wurden die Handelswege im komplexer, Steuerrecht und Abgaben wie Wegezölle taten ihr übriges. Ich denke so Rechnungen wie 1/10 + 3/20 + 4/11 + 1/144 waren damals wie heute nicht gerade beliebt. Das Problem waren dabei natürlich die unterschiedlichen Nenner. Taschenrechner gab es damals noch nicht.
Um das zu vereinfachen wurde um 1600 die Prozentrechnung eingeführt. Prozent leitet sich vom lateinischen „pro centro“ ab. Die Abkürzung „cto“ ist zum heutigen % Zeichen geworden. C und o sich die beiden Kringel, das t ist zum Schrägstrich geworden.
Die Rechnung oben sieht dann so aus: 10% + 15% + 36% + 0,7% . Das sieht schon wesentlich einfacher aus. Diese viel einfachere Rechenweise hat sich damals in recht kurzer Zeit im ganzen deutschen Raum durchgesetzt.
Die Brüche
Die Schreibweise 10% ist eine Abkürzung für 10/100. Das kann gekürzt werden zu 1/10 und als Dezimalzahl 0,1 geschrieben werden.
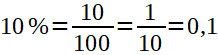
Alle 4 Ausdrücke beschreiben ein und denselben Anteil vom Ganzen. Wenn irgendwo 10% steht, kann also statt der 10% auch 10/100, 1/10 oder 0,1 eingesetzt werden. Die Rechnung bleibt die selbe, sie sieht nur etwas anders aus.
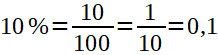
Das Ganze
Wo es Brüche gibt, da gibt es auch Ganze. Bei den Brüchen ist ein Ganzes gleich 1/1 oder einfacher gesagt 1. Wenn wir das 1/1 mit 100 erweitern, dann erhalten wir 100/100. Dies umgewandelt in die Prozentschreibweise ergibt dann 100%. Dieses Ganze wird in der Prozentrechnung Grundwert genannt. Der Grundwert ist immer 100% oder ein Ganzes. Der Grundwert spielt eine zentrale Rolle bei der Prozentrechnung. Wichtig für uns ist, das wir erkennen was der Grundwert ist.
Nehmen wir mal den Satz: „15% aller Gummibären sind rot und in einer Tüte sind 400 Gummibären“.
Wir zerpflücken jetzt mal den Satz in alle seine Einzelteile. Wir haben 15% rote Gummibären, also 15 von 100 Gummibären sind rot. Das Ganze ist die komplette Tüte mit den 400 Gummibären.
Wenn wir jetzt wissen wollen, wieviel rote Gummibären wir haben, dann rechnen wir:
15% von der ganzen Tüte
15% von 400 Gummibären
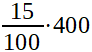
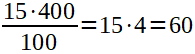
Das ganze könnt ihr natürlich auch mit dem Dreisatz rechnen.
| 400 | 100% | dann geteilt durch 100 |
| 4 | 1% | dann mal 15 |
| 60 | 15% | rote Gummibären |
Begriffe
| Begriff | Bedeutung | Beispiel |
|---|---|---|
| Grundwert | das Ganze | 400 Gummibären |
| Prozentsatz | Anteil vom Ganzen in Hunderstel | 15% |
| Prozentwert | der Anteil als Wert | 60 rote Gummibären |
Bei jeder Prozentrechnung tauchen alle Begriffe auf. Das blöde ist, dass diese Begriffe sich manchmal tarnen. Am einfachsten ist der Prozentsatz zu erkennen, es steht das % Zeichen dahinter. Prozentwert und Grundwert haben oft eine Einheit wie kg oder € oder sie stehen ohne alles da. Da müsst ihr den an Hand der Aufgabe erkennen was was ist. Bei manchen Textaufgaben ist diese Zuordnung der schwierigste Teil.
Beispiel Warenwert
Der Warenwert beträgt 500 € zuzüglich 19% MwSt. ergibt sich der Endpreis.
Hier ist der Warenwert der Grundwert. Die 19% Mehrwertsteuer sind der Prozentsatz. Das Wort „zuzüglich“ bedeutet dass etwas dazukommt. Nämlich der Prozentwert kommt zu den Grundwert dazu. Beide zusammen ergeben den Endpreis.
In Prozente ausgedrückt: 100% + 19% = 119%
In Euro ausgedrückt: 500 € + 95 € = 595 €
500 € ist der Grundwert, 19% der Prozentsatz, 95 € der Prozentwert und 595 € ist die Summe aus Grundwert und Prozentwert.Der Endpreis ist 595 €.
Beispiel MP3-Player
Der MP3-Player „superboom“ kostete früher 40 €. Er ist jetzt 20% günstiger geworden. Wieviel kostet er jetzt?
Der alte Preis ist der Grundwert, die 20% der Prozentsatz. Der Begriff „günstiger geworden“ bedeutet das etwas weniger geworden ist, der Preis in diesem Fall. Der neue Preis ist also der alte Preis minus 20%.
In Prozente ausgedrückt: 100% - 20% = 80%
In Euro ausgedrückt: 40 € - 8 € = 32 €
40 € ist der Grundwert, 20% der Prozentsatz, 8 € der Prozentwert und 32 € ist die Differenz aus Grundwert und Prozentwert. Der MP3-Player kostet jetzt 32 €.
Beispiel USB-Stick
Der USB-Stick ist 5 € günstiger geworden und kostet jetzt 15 €. Um wieviel % ist der Preis runter gegangen?
Auch hier ist der alte Preis der Grundwert. 5 € sind der Prozentwert. 15 € ist die Differenz aus Grundwert und Prozentwert. Wir kennen weder den Grundwert noch den Prozentsatz. Aber der Grundwert ist einfach zu errechen. Der USB-Stick ist günstiger geworden, also war er vorher teurer.
15 € + 5 € = 20 €
20 € sind der Grundwert. 5 € der Prozentwert.
Lösen mit Bruchrechen:
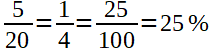
Lösen mit Dreisatz:
| 20 € | 100% | geteilt durch 100 |
| 0,2 € | 1% € | wie oft geht 0,2 in 5 |
| 5 € | 25% | tadaaa :) |
Was gar nicht geht
Früher war der Zinssatz 4%, jetzt ist er 5%, das sind 25% mehr.
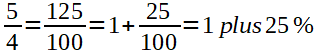
Sieht doch nett aus. Ist aber vollkommen falsch!
In einer Aufgabe beziehen sich alle Prozente immer auf den selben Grundwert. In diesem Fall auf das Kapital. Ein Prozentsatz kann niemals ein Grundwert sein. Der Satz von oben muß also richtig lauten:
Früher war der Zinssatz 4% jetzt ist er 5%, das ist 1% mehr.
Und manchmal geht es doch
Der Preis für ein Fahrrad lag zu Anfang bei 500 €. Dann wurde der Preis um 10% gesenkt. Zwei Wochen später dann um 20% angehoben.
Auch hier kann man einfach aber falsch rechnen:
100% - 10% + 20% = 110%
500 € - 50 € + 100 € = 550 €
Leider darf man in diesem Fall nicht so einfach rechnen. Wenn wir die Aufgabe Schritt für Schritt betrachten wird klar, warum das so ist.
1. Die Preissenkung: 100% - 10% = 90% oder 500 € - 50 € = 450 €
Nach der Preissenkung beträgt der Preis 450 €
2. Die Preissteigerung: 100% + 20% = 120% oder 450 € + 90 € = 540 €
Für die Preissteigerung wurde der Preis nach der Preissenkung als Grundwert genommen. Weil zu diesem Zeitpunkt das der aktuelle Preis ist. Bei Aufgaben wo zeitlich nacheinander Sachen passieren, da muß man immer mit dem aktuellen Preis als Grundwert rechnen.
Ein anderes Beispiel für dieses schrittweise Rechnen ist ein Sparbuch. Die Zinsen werden immer auf das aktuell vorhandene Guthaben gerechnent. Nicht auf Werte die früher irgendwann mal gültig waren.
Zusammenfassung
Prozentrechnung ist also einfache Bruchrechnung, man sieht es nur nicht sofort. Der Nenner 100 ist versteckt im Zeichen %.
Die wichtigste Frage ist: Was ist der Grundwert? oder auch: Was sind die 100% ?
Es kommen oft Summen oder Differenzen aus Grundwert und Prozentwert vor. Zu erkennen an Wörtern wie: inclusive, zuzüglich, teurer, billiger und viele andere.