Rechenregeln der Potenzen

Dies ist eine kompakte Übersicht der Rechenregeln für Potenzen, Wurzeln und Logarithmen. Es geht rund um den folgenden Ausdruck: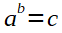
a^b=c .

Wenn der Potenzwert c gesucht ist => Potenz,

wenn die Basis a gesucht ist => Wurzel,

wenn der Exponent b gesucht ist => Logarithmus.

Potenzen

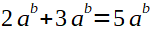2a^b+3a^b=4a^b Addieren gleiche Basis, gleicher Exponent

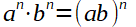a^n*b^n=(ab)^n Multiplizieren gleicher Exponent

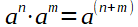a^n*a^m=a^(n+m) Multiplizieren gleiche Basis

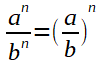
a^n/b^n=(a/b)^n

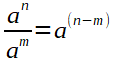
a^n/a^m=a^(n-m)

a^-n=1/a^n

(a^n)^m=a^(n*m)

a^0=1

a^1=a

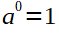
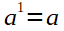
Wurzeln

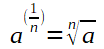
a^(1/n)=n wurzel a

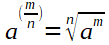
a^(m/n)=n wurzel (a^m)

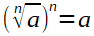
=(n wurzel a)^n=a

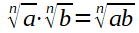
=n wurzel a*n wurzel b=n wurzel ab

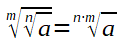
=m wurzel n wurzel a=n*m wurzel a

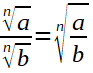
=n wurzel a / n wurzel b=n wurzel a/b

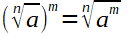
=(n wurzel a)^m =n wurzel a^m

Logarithmen

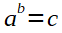a^b=c kann umgeformt werden zu: 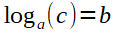log_a(c)=b und auch wieder zurück

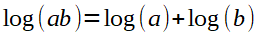
log(ab)=log(a)+log(b)

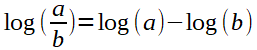
log(a/b)=log(a)-log(b)

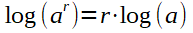
log(a^r)=r*log(a)

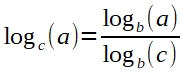log_c(a)=log_b(a) / log_b(c) Basiswechsel von der Basis c zur Basis b

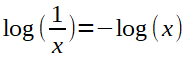
log(1/x)=-log(x)

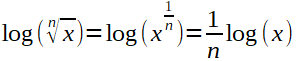
log( nroot{n}{x})= log(x^ {{1} over {n}} )= {1} over {n} log( x)

Bitte beachten:

An einigen Stellen dürfen die Werte nicht 0 sein, weil die Division durch Null verboten ist. An anderen Stellen dürfen keine negativen Werte auftauchen. Z.B.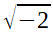 wurzel -2 wäre nur möglich wenn man statt mit realen Zahlen, mit komplexen Zahlen rechnet.
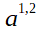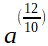Und nicht vergessen die Dezimalzahlen, a^1,2 ist zwar ein gültiger Term, aber 1,2 ist ein Dezimalbruch. In der Bruchschreibweise sieht es dann so aus: a^(12/10) .
Wenn ich in einem Term log() ohne Basis angegeben habe, dann ist damit gemeint das alle log() in dem Term/Gleichung die selbe Basis haben.